
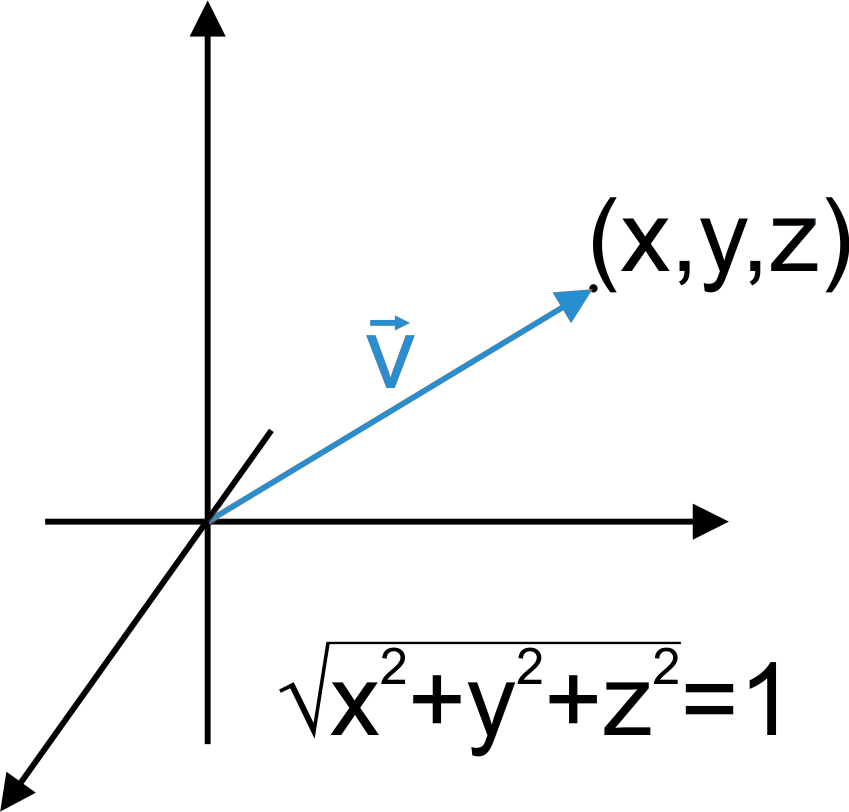
If we have the information about the following elements, then we can determine the angle between a line and the plane using the formula below: This phenomenon is shown in the figure below as it shows the angle between a line r and a plane. In other words, we can say that the angle between a straight line and a plane is an angle formed between the line and its orthogonal projection on the plane. This angle that is formed between the line and a plane is actually the angle formed by the straight line with its orthogonal projection on the plane.
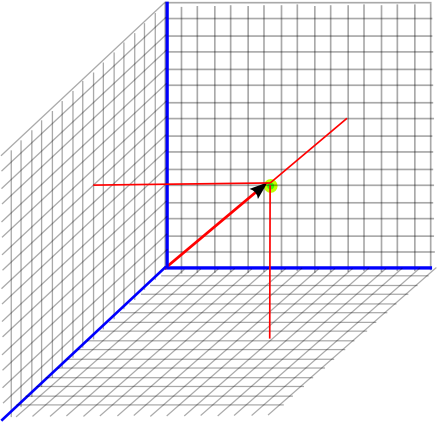
If the straight line is present on the plane or is parallel to it, then the angle formed between the line and plane will be 0 degrees.The angle formed between the plane and a straight line will be different in each of the above three circumstances.
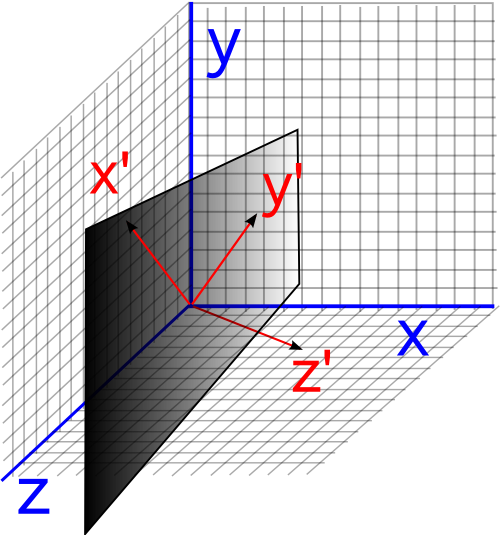
There can be the following three scenarios when a straight line and the plane can exist together: This angle between a line and a plane is equal to the complement of an angle between the normal and the line. For example, if you draw something on a flat paper, then it means that you are drawing something on a plane.Īn angle between a line and a plane is formed when a line is inclined on a plane, and a normal is drawn to the plane from a point where it is touched by the line. It is also a 2-D figure because like a straight line, it does not have any thickness, rather it has only length and width. A plane is a flat surface that is formed when an infinite number of points extend without limits in any direction.


 0 kommentar(er)
0 kommentar(er)
